b High Magnetic Field Laboratory,
Max-Planck-Institut für Festkörperforschung and
Centre National de la Recherche Scientific,
BP 166, F-38042 Grenoble, Cedex 9, FRANCE.
c L.D.Landau Institute for Theoretical Physics,
Kosygina 2, Moscow, Russia.
In the single-electron approximation of the Two Dimensional Electron Gas (2DEG) under strong magnetic fields, the spin up and spin down electron states are separated by an energy gap equal to the "bare" Zeeman spin splitting energy: g mBB, where g is the "bare" g-factor, which is different from the free electron g-factor, g0 due to the crystall fields. The low lying excitations are electron-hole pairs of opposite spins, having, due to the electron-electron interactions, a nonzero kinetic energy and strong k-dispersion (spin-excitons, [2,3]). This results in a strong enhancement (up to a factor of 10, as is the case in GaAs) of the effective g(k) -factor.
Due to the Coulomb interaction the spin-excitons are bound states of electron-hole pairs, which unlike the individual electrons or holes, can propagate rather freely under the influence of the magnetic field due to their zero electric charge. These elementary excitations are, therefore, chargeless particles with nearly parabolic dispersion in the low-k limit [2]. At k = 0 there exist a gap equal to the "bare" Zeeman splitting.
Experimental observation of spin-excitons is a challenging problem, since an additional spin should be involved, in order to satisfy the spin conservation requirement in the excitation process. A good candidate can be the nuclear spin, which is coupled to the electron spin by the hyperfine interaction [4]. Effectiveness of the (Fermi) contact hyperfine interaction in the quantum Hall effect regime was intensively studied recently both theoretically [5,6,7] and experimentally [8,9,10].
Existence of the energy gap at k = 0, severly impedes, hovewer, creation of spin excitons by nuclear spins [7], because the electron Zeeman splitting is orders of magnitude larger than the nuclear Zeeman splitting. Here we show, that a periodic external potential can remove the energy gap in the spin-exciton dispersion at certain values of the spin-exciton momenta.
This may result in several interesting phenomena. First, the rate of nuclear spin depolarization processes, such as nuclear spin diffusion, [11] will be strongly enhanced. Second, since the process of electron spin polarization is also strongly enhanced, an external rf pulse can polarize effectively the entire spin system, thus creating a dense, long living spin-polarized plasma, where condensation into a collective spin density wave ground state may take place.
In this paper we focus on the formation of a single gapless spin exciton in spin-polarized, periodically modulated 2DEG under a strong magnetic field.
It is well known that the spin-exciton dispersion in a homogeneous sample is [2,3]:
| (1) |
Espex([k\tilde]2) » esp+1/4ec[k\tilde]2, have a gap equal to the bare Zeeman spin splitting energy.
Application of an external electric field, which couples to the electrical dipole moment of the electron-hole system [10]can remove this energy gap. A more interesting possibilty may arise if one uses a novel technique, in which the 2DEG is exposed to artificially generated periodic potential with periods in the submicron range [12,13,14,15]. These wavelenghts are much longer than the magnetic length lB, but the amplitude V0 of the potentials is, typically, in the range of V0 ~ 1meV,which is much larger than the exciton gap esp.
It is easy to see why this energy gap can be removed by the modulation potential in an ideal model of noninteracing electrons: Consider a noninteracing electron-hole pair with opposite spins,which are subject to an external magnetic field and a periodic potential with amplitude V0 and period a (Inset to Fig.(1)). By appropriately selecting the spatial separation between the electron and the hole along the modulation direction (say the x-axis, see inset in Fig.(1)) the energy difference between them can be reduced to zero. The minimal amplitude V0 required to satisfy this condition is 1/2esp, the spatial separation between the electron and the hole involved is half of the modulation period a,and the corresponding wave number (along the y-direction) is ky = a/2lB2.
The picture is significantly more complicated,however,in the presence of the strong Coulomb interaction,where bound spin-excitons exist. In particular,the large Coulomb interaction induced enhancement of the effective g-factor at k ~ a/2lB2 may pose a seriouse obstacle to the desired formation of gapeless excitations.
To address this problem we should investigate in detail our periodically modulated system with a single spin exciton, where the e-h interaction is taken into account.
Consider a 2DEG under a strong perpendicular magnetic field [B\vec] = Ñ×[A\vec],where [A\vec] is the vector potential given in the Landau gauge. Assuming that the filling factor is close to
n = 1,the chemical potential is in between the Zeeman spin split energy gap and the noninteracting electron gas is in a spin polarized ground state.Applying a modulated potential of the form
| (2) |
| (3) |
e(0) ,¯ º 1/2((h/2p) wc -±gmB B) - m ,¯ with m ,¯ the chemical potential for the respective energy level, wc º [eB/( m*c)], [^H]int is the electron-electron interaction Hamiltonian, and [^(r)] ([q\vec]) is the charge density fluctuation operator:
| (4) |
Here [^a]fp is a creation operator of an electron in the lowest Landau level with an orbital center wave number p (i.e. Landau orbital eipyf0([x/( lB)] + plB)) with spin and [^b]pf is a creation operator of an electron in the same orbital state but with spin ¯.
The interaction Hamiltonian [^H]int may be written in the compact form [17]:
| (5) |
| (6) |
One may introduce ßpin" density operators:
| (7) |
The Hamiltonian, Eq. (3) can be diagonalized exactly in the special case when the ground state |0ñ of the underlying noninteracting electrons system is at filling factor n = 1,that is when
[^a]pf|0ñ = 0,and
[^b]p|0ñ = 0 for any orbital p. Under this condition the spin density operators [^[S\vec]]([k\vec]) º [^S]x ([k\vec]) - i[^S]y ([k\vec]) as projected onto |0 > , can be regarded as creation operators of spin excitons: [^A]f[k\vec] º [^S]([k\vec]) (note that they satisfy the usuall Bose-Einstein commutation relations, when applied to the ground state |0ñ).
Constructing a superposition of spin excitons:
| (8) |
| (9) |
Thus |yexñ is an eigenstate of the Hamiltonian [^H] with energy E if the coefficients f([k\vec]) satisfy the equations:
| (10) |
Specifying the modulation potential U(x) (Eq.2) the above equations reduce to:
| (11) |
A Fourier transform of this equation with respect to kx,that is:
| (12) |
|
Expanding eex to first order in (i[(¶)/( ¶x)])2, Eq.(12) reduces to a 1D Schr[o\ddot]dinger equation for a particle in a periodic potential, which has the well known Bloch-like solution: [f\tilde]a (x,ky) = eiax ua (x,ky), where ua (x,ky) is a periodic function of x.
This Bloch's form remains a valid solution of Eq.(12) also in the general case, where the expansion in (i[(¶)/( ¶x)])2 may not be terminated at any finite order, since the lattice translation operator ea [(¶)/(¶x)] commutes with the spin-exciton ënergy operator"
eex [(i[(¶)/(¶x)])2 + ky2].
Eq.(11) is thus equivalent to the eigenvalue problem of the hermitian matrix B defined by:
| (13) |
bn º eex((a+ nK0)2+ky2), and n,n¢ = 0,±1,...
Typical values of the period a of the modulation potential are in the range 1-5×103A.For magnetic fields in the range B = 3.5-6T,the magnetic length lB = 104-136A,and
esp » 0.4-0.7 meV,ec » 9-12 meV.The value of the amplitude V0 was estimated by Winkler et.al [12] to be about 5 meV for a gate voltage Vg ~ 1V.
For sufficiently small [k\tilde]y for which |b| << 1, the lowest eigenvalue of the full matrix B , which corresponds to a = 0, may be approximated by considering the three coupled channels n = 0,±1 . This yields:
| (14) |
[k\tilde]y[K\tilde]0 £ 4p, e([k\tilde]y) can be computed numerically quite accurately by trancating the matrix B into a relatively small (i.e. 20×20) submatrix. The results of both procedures are plotted in Fig.(1):

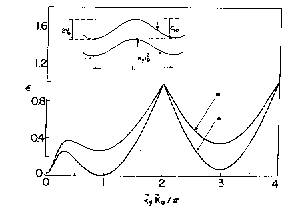
Fig.1 . The energy dispersion(along the direction perpendicular to the modulation axis) of the lowest energy band of a single spin exciton. The lower curve (a) represents the result of very accurate diagonalization of the matrix (13),whereas the upper curve (b) was obtained from the approximate formula (14). The values of parameters used are: [k\tilde]0 = 0.4, [V\tilde]0 = 0.465, [(e)\tilde]sp =0.03.
The dispersion curve e([k\tilde]y) has minima close to the maxima of |b|,i.e. close to the maxima of |sin([K\tilde]0[k\tilde]y/2)|, which occure at ky lB2 = na/2, n = 1,3,5,... . This is clearly seen from the approximate expression for e([k\tilde]y), Eq.(14), which has minima at the same points. The spike-like maxima at [k\tilde]y[K\tilde]0/p = 2n (i.e. ky lB2 = na,only that for n = 1 is shown), correspond to the zeros of b,at which points the energy is identical to the free exciton energy at kx = 0 with
[k\tilde]y = 2pn/[K\tilde]0 >> 1.
As expected from the simple consideration sketched in the inset to Fig.(1), as well as from Eq.(14),the minima of the dispersion curve get deeper by increasing the amplitude [V\tilde]0. At some critical value of [V\tilde]0 the first minimum touches the zero excitation energy level (for the values of the parameters used it was always the minimum close to ky lB2 = a/2). The critical value obtained in Fig.(1) is [V\tilde]0c = .465, i.e. Voc ~ 5 meV, which is a reasonable number, experimentally.
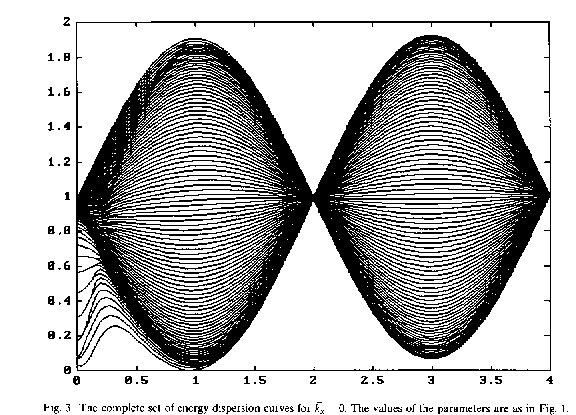
The complete spectrum of the single spin exciton can be obtained by computing the whole set of eigenvalues of the matrix B as functions of ky and the Bloch's wave number kx º a in the first Brillouin zone K0/2 > a ³ -K0/2. For a given ky, the lower part of the spectrum has a usual one-dimensional band structure (see Fig.(2)).

However,in contrast to the usual parabollic free particle dispersion, the full energy dispersion of a free spin exciton is bound by the Coulomb energy, ec. Thus the infinite number of bands in the upper part of the spectrum accumulate into an infinitely dense manifold.
In particular for ky = 0, the effective lattice potential vanishes,(b=0), and the spectrum has a single accumulation point at
e = 1 + [(e)\tilde]sp. This expands into a finite region of accumulation points as ky gets larger (Fig.(2)).
Of special interest here are the spectra above the absolute minimum at [k\tilde]y = p/[K\tilde]0, and the higher local minima at
[k\tilde]yn = (2n+1)p/[K\tilde]0, n = 1,2,..., (see Fig.(3)). In considering these projections of the entire spectrum on the kx = 0, [k\tilde]yn lines,we would like to estimate the size of the broad continuous regions appearing there and the density of levels within each band. Furthermore,we would also like to understand the difference between the structure of the projected spectrum at n = 0 and that at n = 1, shown in Fig.(3).
Due to the smallness of [K\tilde]0 the values of all [k\tilde]yn are quite large (the smallest one [k\tilde]y 0 = p/[K\tilde]0 = 7.85). Thus the n-dependent term in the diagonal elements of matrix B, dn = e-[k\tilde]n2 /4I0 ([k\tilde]n 2 /4), with [k\tilde]n 2 = (n[K\tilde]0)2 +[k\tilde]y 2, can be approximated by the asymptotic formula dn » Ö([2/( p)])/[k\tilde]n for any value of n.
The components An of an eigenvector of matrix B satisfy the recursion relation:
| (15) |
nc = Ö3[k\tilde]y /[K\tilde]0, and approximate all dn for n < nc by the constant d0 (the central domain), whereas all dn for n > nc are replaced by zero (the asymptotic domain). The asymptotic domain consists of an infinite number of diffraction channles n,and is therefore associated with the continuous part of the spectrum. The central domain, contains only a finite number of channels,and is responsible for the few discrete energy levels observed below,as well as above,the broad continuum in Fig.(3). This domain becomes considerably narrower with the increasing order n,and is therefore seen clearly only at n = 0.
Thus we have a three-diagonal matrix with constant diagonal terms
b = 1+[(e)\tilde]sp-d, as well as constant off-diagonal ones-b, in both domains, where d = d0 in the central domain,and
d = 0 in the asymptotic one. Eq.(15) can be then trivially solved (seperately in each domain) by the ansatz An = tn if
t = t± º [i(e- b)±Ö(4b2 -(e-b)2)]/2b, which satisfy t+t- = -1. These solutions yield bound values (on the unity circle) for tn if 4b2 -(e-b)2 > 0. In this case we may define a real variable x0 by eiK0 x0 º t±, and solve for the energy to obtain:
| (16) |
1+[(e)\tilde]sp-2b < e < 1+[(e)\tilde]sp+2b. The density of levels n(e) in this band is proportional to
| (17) |
In the central domain,
b = 1+[(e)\tilde]sp-d0,the number of channels is finite,and the spectrum is discrete,bound between emin º 1+[(e)\tilde]sp-2b-d0 and (1+[(e)\tilde]sp-2b) (bottom) ,and between (1+[(e)\tilde]sp+2b-d0) and emax º 1+[(e)\tilde]sp+2b (top). Using the numerical values of the relevant parametrs we find for n = 0, emin = .005 and emax = 1.85,in excellent agreement with our numerical results shown in Fig.(3).
It should be stressed at this point that the method proposed here for estimating the spectrum boundaries and the density of levels in the continuous regions is valid everywhere along the [k\tilde]y axis, provided [k\tilde]y is large enough to ensure the asymptotic approximation for dn. The simple analytical expression for emin, derived above,enables us to get a rather accurate estimate of the critical amplitude, [V\tilde]0,c, of the modulation potential, for which the spectrum becomes gapless,that is:
| (18) |
The occurence of a gapless spectrum for independent spin excitons,in which the zero energy corresponds to a finite (and large) wavenumber,ky,0,should have several interesting consequences. First of all, such gapless, mobile,spin excitons may easily depolarize the nuclear spins via the hyperfine interaction,thus leading to enhanced nuclear spin-lattice relaxation , [7,9] and nuclear spin diffusion, [10,11] in the system.
Second,a (dense) polarized nuclear spin system,which may be generated by an external rf pulse,can polarize effectively the entire (much more dilute) electron spin system,thus creating a plasma of gapless spin-excitons,which may condense into a collective Spin Density Wave ground state,with a finite wavelength.
The description of such a system of many,finite wavelength,spin excitons is a complicated problem since the density operators (7) at finite wavevectors do not obey the standard spin commutation relations, implying in particualr that the spin excitons near ky,0 are strongly interacting quasi-particles.
To summarize, we have studied the two-dimensional electron gas under strong magnetic field in external periodic potential with wave lengths in the submicrometer range and amplitues of the order of a few meV and have shown the possibility of creating gapless spin-exitons in such a system. This may result in strong enhancement of the nuclear spin depolarization processes via the hyperfine interaction between the electron and the nuclear spin systems. We have also discussed briefly the posibility that a dense plasma of gapeless spin excitons can condense into a Spin-Density-Wave ground state.
We are gratefull to P. Wyder for constructive discussions and stimulating support during this work and to G. Kventzel for illuminating remarks.
This paper was completed during Yu.B. stay in France due to an agreement between Ecole Normale Superieure and L.D.Landau Institute for Theoretical Physics.
This research was supported by a grant from the German-Israeli Foundation for Scientific Research and Development,No. I-0222-136.07/91, and by the fund for the promotion of research at the Technion.
WebMaster RK
